개요
강의(질문) - 복습(필기) - 자료화
출처
https://www.youtube.com/watch?v=DHYLMwqa9oc&t=5s
학습목표
출처
https://www.youtube.com/watch?v=DHYLMwqa9oc&t=5s
학습목표
- 선형 회귀의 분류 원리에 대해 이해할 수 있다.
- 선형 회귀의 모델 파라미터를 계산할 수 있다.
- 모델이 가정하고 있는 선형성에 대해서 이해할 수 있다.
선형 회귀 모델
회귀 모델의 정의
- 한 개의 종속 변수(dependent variable)와 설명 변수들(explanatory variable(s))과의 관계를 모델링
- 종속 변수, 설명 변수에 따라 값이 달라지는 결과 변수
- 설명 변수, 원인이 되는 변수
- ex) 설명 변수: 겨울철 강수량, 재배철 평균 기온, 수확기 강수량
종속 변수: 와인품질 - 종속 변수와 설명 변수들의 관계를 정의하기 위해 방정식 사용
- 수치적(numerical) 종속 변수
- 한 개 또는 그 이상의 수치적 설명 변수
- 예측 & 추정 시에 사용
- 설명 변수들이 수치값을 갖고 회귀 분석 모델을 통해서 종속 변수를 알아내는 과정을 예측, 추정이라 함
선형성이란
어느 변수들 사이의 관계를 1차 방정식의 관계로 나타낼 수 있다면 선형성을 띄고 있다고 볼 수 있다.
변수들 사이의 관계 - 선형 함수
회귀 모델의 예측 대상
종속 변수는 설명 변수에 따라서 다양한 값을 가질 수 있다. 와인의 등급을 예측하는 예를 통해 선형 회귀 모델을 만드는 방법을 알아보자.
회귀 모델을 만들기 위해서는 데이터를 측정해야 한다. 와인의 등급을 예측하기 위한 모델을 만들기 위해서는 와인, 와인의 등급, 와인이 만들어진 시기의 강수량, 기온, 토양의 질 등 다양한 정보를 수집해야 한다.
이 때, 우리가 볼 수 있는 모든 와인과 등급을 모집단(참값)이라고 한다. 그리고 그 중 우리가 모을 수 있는 일부의 와인과 등급을 무작위 샘플(관측 값)이라고 한다.
와인의 등급을 결정짓는 실제 규칙이 존재한다고 가정할 때, 우리가 구하고자 하는 모델이 그 실제 규칙을 나타내는 함수라고 할 수 있다. 와인의 등급을 매기는 실제 규칙이 존재하더라도 와인 감별사에 의해 등급이 달라질 수 있는데 이를 규칙에 반영하기 위해 무작위 에러(노이즈)값을 지정한다.
우리는 무작위 샘플을 통해 실제 규칙과 비슷한 생성 규칙을 만들 수 있습니다. 하지만, 실제 규칙과 예상 규칙은 같지 않으므로 다른 변수를 통해 예측 규칙을 나타낼 수 있습니다.
선형 회귀 모델의 확률적 관점
일부 데이터를 가지고 선형 회귀 모델을 추론한다면 항상 정확한 규칙을 맞출 수는 없다. 실제 규칙과는 조금씩 차이가 생긴다. 제대로 된 회귀 모델을 만드려면 차이(error)를 최소화해야 한다.
어느 변수들 사이의 관계를 1차 방정식의 관계로 나타낼 수 있다면 선형성을 띄고 있다고 볼 수 있다.
변수들 사이의 관계 - 선형 함수
회귀 모델의 예측 대상
종속 변수는 설명 변수에 따라서 다양한 값을 가질 수 있다. 와인의 등급을 예측하는 예를 통해 선형 회귀 모델을 만드는 방법을 알아보자.
회귀 모델을 만들기 위해서는 데이터를 측정해야 한다. 와인의 등급을 예측하기 위한 모델을 만들기 위해서는 와인, 와인의 등급, 와인이 만들어진 시기의 강수량, 기온, 토양의 질 등 다양한 정보를 수집해야 한다.
이 때, 우리가 볼 수 있는 모든 와인과 등급을 모집단(참값)이라고 한다. 그리고 그 중 우리가 모을 수 있는 일부의 와인과 등급을 무작위 샘플(관측 값)이라고 한다.
와인의 등급을 결정짓는 실제 규칙이 존재한다고 가정할 때, 우리가 구하고자 하는 모델이 그 실제 규칙을 나타내는 함수라고 할 수 있다. 와인의 등급을 매기는 실제 규칙이 존재하더라도 와인 감별사에 의해 등급이 달라질 수 있는데 이를 규칙에 반영하기 위해 무작위 에러(노이즈)값을 지정한다.
우리는 무작위 샘플을 통해 실제 규칙과 비슷한 생성 규칙을 만들 수 있습니다. 하지만, 실제 규칙과 예상 규칙은 같지 않으므로 다른 변수를 통해 예측 규칙을 나타낼 수 있습니다.
선형 회귀 모델의 확률적 관점
일부 데이터를 가지고 선형 회귀 모델을 추론한다면 항상 정확한 규칙을 맞출 수는 없다. 실제 규칙과는 조금씩 차이가 생긴다. 제대로 된 회귀 모델을 만드려면 차이(error)를 최소화해야 한다.
파라미터 예측: 최소 제곱 방법
그렇다면 어떻게 해야 가진 데이터로 최선의 회귀 모델을 만들 수 있는가?
최소 제곱
최소 제곱
- 최적의 모델은 실제 Y값과 예측된 Y 값의 차이 (에러)가 최소가 되어야 함
- 에러의 값은 무조건 양수이어야 하므로 제곱을 시킴
- 최소 제곱 방법은 에러의 제곱의 합(Sum of the Squared Errors, SSE)을 최소화 시킴
- 에러의 제곱의 합을 최소화 시킬 수 있는 파라미터를 찾으면 적절한 회귀 모델을 만든 것임
최소 제곱의 해
예측 방정식에 따른 기울이과 y 절편 구하는 방법을 알아보자.
Y 절편 구하기
Y 절편을 구하기 위해서 error^2의 합을 미분한다.
알고자하는 파라미터가 베타_0와 베터_1이기 때문에 베타_0와 베타_1에 대한 error^2의 합의 변화량을 알면, 적합한 파라미터를 계산할 수 있다.
선형 회귀 모델로는 안 풀리는 문제들
선형성의 한계
다른 모델을 통해 해결할 수 있음
다른 모델을 통해 해결할 수 있음







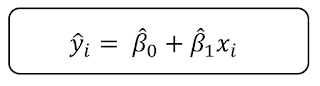




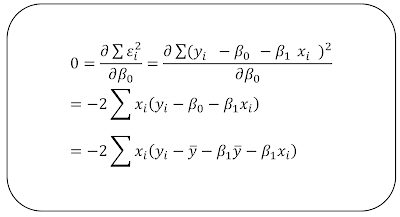


댓글 없음:
댓글 쓰기